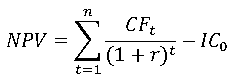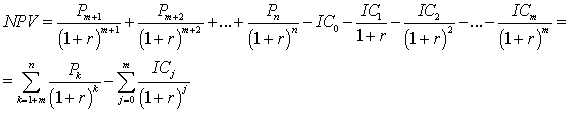Чистая приведённая стоимость — Википедия
Чистая приведённая стоимость (ЧПС, чистый приведённый эффект, чистая текущая стоимость, чистый дисконтированный доход, ЧДД, англ. Net present value, NPV) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню. Показатель NPV представляет собой разницу между всеми денежными притоками и оттоками, приведёнными к текущему моменту времени (моменту оценки инвестиционного проекта). Он показывает величину денежных средств, которую инвестор ожидает получить от проекта, после того, как денежные притоки окупят его первоначальные инвестиционные затраты и периодические денежные оттоки, связанные с осуществлением проекта. Поскольку денежные платежи оцениваются с учётом их временно́й стоимости и рисков, NPV можно интерпретировать как стоимость, добавляемую проектом. Её также можно интерпретировать как общую прибыль инвестора.
Согласно американскому профессору Энтони Аткинсону чистая приведённая стоимость — сумма всех дисконтированных денежных потоков (притоков и оттоков), связанных с инвестиционным проектом
Для потока платежей CF (Cash Flow), где CFt{\displaystyle CF_{t}} — платёж через t{\displaystyle t} лет (t=1,…,N{\displaystyle t=1,…,N}) и начальной инвестиции IC (Invested Capital) в размере IC=−CF0{\displaystyle IC=-CF_{0}} чистая приведённая стоимость NPV{\displaystyle NPV} рассчитывается по формуле:
- NPV=∑t=0NCFt(1+i)t=−IC+∑t=1NCFt(1+i)t{\displaystyle NPV=\sum _{t=0}^{N}{\frac {CF_{t}}{(1+i)^{t}}}=-IC+\sum _{t=1}^{N}{\frac {CF_{t}}{(1+i)^{t}}}},
- где i{\displaystyle i} — ставка дисконтирования.
В обобщённом варианте, инвестиции также должны дисконтироваться, так как в реальных проектах они осуществляются не одномоментно (в нулевом периоде), а растягиваются на несколько периодов. Расчёт ЧПС — стандартный метод оценки эффективности инвестиционного проекта и показывает оценку эффекта от инвестиции, приведённую к настоящему моменту времени с учётом разной временно́й стоимости денег. Если ЧПС больше 0, то инвестиция экономически эффективна, а если ЧПС меньше 0, то инвестиция экономически невыгодна (то есть альтернативный проект, доходность которого принята в качестве ставки дисконтирования требует меньших инвестиций для получения аналогичного потока доходов).
С помощью ЧПС можно также оценивать сравнительную эффективность альтернативных вложений (при одинаковых начальных вложениях более выгоден проект с наибольшим ЧПС). Но всё же для сравнительного анализа более применимыми являются относительные показатели. Применительно к анализу инвестиционных проектов таким показателем является внутренняя норма доходности.
В отличие от показателя дисконтированной стоимости при расчёте чистого дисконтированного дохода учитывается начальная инвестиция. Поэтому формула чистого дисконтированного дохода отличается от формулы дисконтированной стоимости на величину начальной инвестиции IC=−CF0{\displaystyle IC=-CF_{0}}.
Положительные свойства ЧПС:
- Чёткие критерии принятия решений.
- Показатель учитывает стоимость денег во времени (используется коэффициент дисконтирования в формулах).
- Показатель учитывает риски проекта посредством различных ставок дисконтирования. Бо́льшая ставка дисконтирования соответствует бо́льшим рискам, меньшая — меньшим.
Отрицательные свойства ЧПС:
- В руководстве ЮНИДО критикуется использование NPV для сравнения эффективности альтернативных проектов (Беренс, Хавранек, 1995, стр.240). Для устранения этого недостатка NPV был разработан индекс скорости удельного прироста стоимости (Коган, 2012).
- Во многих случаях корректный расчёт ставки дисконтирования является проблематичным, что особенно характерно для многопрофильных проектов, которые оцениваются с использованием NPV.
- Хотя все денежные потоки (коэффициент дисконтирования может включать в себя инфляцию, однако зачастую это всего лишь норма прибыли, которая закладывается в расчётный проект) являются прогнозными значениями, формула не учитывает вероятность исхода события.
Для того чтобы оценить проект с учётом вероятности исхода событий поступают следующим образом:
Выделяют ключевые исходные параметры. Каждому параметру устанавливают ряд значений с указанием вероятности наступления события. Для каждой совокупности параметров рассчитывается вероятность наступления и NPV. Дальше идёт расчёт математического ожидания. В итоге получаем наиболее вероятностное NPV.
Корпорация должна решить, следует ли вводить новые линейки продуктов. Новый продукт будет иметь расходы на запуск, эксплуатационные расходы, а также входящие денежные потоки в течение шести лет. Этот проект будет иметь немедленный (T = 0) отток денежных средств в размере $ 100 000 (которые могут включать в себя механизмы, а также расходы на обучение персонала). Другие оттоки денежных средств за 1-6 лет ожидаются в размере $ 5000 в год. Приток денежных средств, как ожидается, составит $ 30 000 за каждый год 1-6. Как только компания получает прибыль от реализации проекта (например, $ 25 000 после первого года), она кладёт их в банк под 10 % годовых на оставшееся до конца проекта время (то есть на оставшиеся 5 лет для первых $ 25 000). Все денежные потоки после уплаты налогов, и на 7 год никаких денежных потоков не планируется. Ставка дисконтирования составляет 10 %.
Таким образом, требуется оценить, какая сумма больше:
- 100000⋅(1+0.1)t≶∑i=1tpi⋅(1+0.1)(t−i){\displaystyle 100\,000\cdot (1+0.1)^{t}\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(t-i)}}, где pi{\displaystyle p_{i}} — доход от проекта, полученный в i-й год реализации проекта, t — общая длительность проекта. Поделим обе части на (1+0.1)t{\displaystyle (1+0.1)^{t}}:
- 100000≶∑i=1tpi⋅(1+0.1)(−i){\displaystyle 100\,000\lessgtr \sum _{i=1}^{t}p_{i}\cdot (1+0.1)^{(-i)}}.
Каждое слагаемое в правой части неравенства — это приведённая стоимость денег по годам. Например, $ 25 000, полученные от реализации проекта после первого года и положенные в банк на 5 лет, дадут такой же доход, как $ 22 727, положенные в банк в начальный момент времени на 6 лет. Таким образом, приведённая стоимость (PV) может быть рассчитана по каждому году:
Сумма всех этих значений является настоящей чистой приведённой стоимостью, которая равна $ 8881.52. Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем класть деньги в банк (под 10 % годовых с капитализацией процентов), и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Тот же пример с формулами в Excel:
- NPV (ставка, net_inflow) + initial_investment
- PV (ставка, year_number, yearly_net_inflow)
При более реалистичных проблемах необходимо будет рассмотреть другие факторы, как расчет налогов, неравномерный денежный поток и ценности, а также наличие альтернативных возможностей для инвестиций.
Кроме того, если мы будем использовать формулы, упомянутые выше, для расчёта NPV — то мы видим, что входящие потоки (притоки) денежных средств являются непрерывными и имеют такую же сумму; и подставив значения в формулу
- 1−(1+i)−ni{\displaystyle {\frac {1-(1+i)^{-n}}{i}}} мы получим 1−(1+0.1)−60.1=4.3553{\displaystyle {\frac {1-(1+0.1)^{-6}}{0.1}}=4.3553}.
И если умножить полученное значение на денежные потоки (CF), и учесть первоначальные затраты, то в итоге вычислим чистую приведённую стоимость (NPV):
- [4.3553(30000−5000)]−100000=$8881.52{\displaystyle [4.3553\,(30\,000-5000)]-100\,000=\$\,8\,881.52}
Поскольку NPV больше нуля, то было бы лучше инвестировать в проект, чем ничего не делать, и корпорации должны вкладывать средства в этот проект, если нет альтернативы с более высоким NPV.
Сравнение эффективности альтернативных проектов[править | править код]
Использование NPV может привести к ошибке при сравнении эффективности разнопараметрических инвестиционных проектов и при формировании портфеля инвестиционных проектов. Под разнопараметрическими понимаются такие проекты, у которых одновременно отличаются три инвестиционных параметра: сумма инвестиций, расчётный период и ежегодные финансовые результаты (Коган, 2012).
Покажем это на следующем примере. Сравним эффективность покупки векселя А и векселя В. Эти сделки можно рассматривать как простейшие инвестиционные проекты с единственным оттоком и единственным притоком. Вексель А стоит 100 тыс.р., его выкупят через три года, заплатив при этом 150 тыс.р. Вексель В стоит 50 тыс.р., его выкупят через два года, заплатив при этом 70 тыс. р. При ставке дисконта 10 %, NPVA{\displaystyle NPV^{A}}= 12,7 тыс.р., что больше, чем NPVB{\displaystyle NPV^{B}}=7,85 тыс.р.
Таким образом, по NPV, проект А эффективнее проекта В. Казалось бы, инвестору выгоднее покупать векселя типа А. Однако, представим, что этот инвестор купит два векселя В. При этом он потратит те же 100 тыс.р., что и для покупки векселя А, но выгод получит больше: NPVB+B{\displaystyle NPV^{B+B}}= 15,7 тыс.р. таким образом, инвестиции в векселя типа В выгоднее, чем инвестиции в векселя типа А.
Эти два проекта отличаются не только по суммам инвестиций, но и по расчётным периодам: покупка векселя А — трёхлетний проект, покупка векселя В — двухлетний проект. Если добавить в анализ и этот фактор, то покупка векселя А выглядит ещё менее выгодной. Так, инвестор, имеющий только 100 тыс.р., за шесть лет сможет только дважды купить вексель типа А (NPV этих двух сделок составит 22,24 тыс.р.), но трижды по два векселя типа В (NPV этих шести сделок составит 39,4 тыс.р.). Таким образом, в результате включения в анализ суммы инвестиций и расчётного периода проектов, векселя типа В выглядят ещё более эффективными, чем векселя типа А.
Из данного примера следует вывод, что для корректного анализа эффективности инвестиций, необходимо учитывать три фактора: NPV, сумму инвестиций и расчётный период проекта. Все эти факторы объединены в индекс скорости удельного прироста стоимости, поэтому при использовании этого показателя не возникают вышеуказанные проблемы.
- ↑ Аткинсон Э.А., Банкер Р.Д., Каплан Р.С., Юнг М.С. Управленческий учёт. — СПб.: ООО «Диалектика», 2019. — С. 504—505. — 880 с. — ISBN 978-5-907144-70-5.
NPV формула расчета пример. NPV инвестиционного проекта
Инвестировать — это значит вложить свободные финансовые ресурсы сегодня с целью получения стабильных денежных потоков в будущем. Вкладываться можно в финансовые инструменты, или в новый бизнес, или в расширение уже существующего бизнеса. В любом случае, инвестирование — это вложение денег в какие-то активы на долгосрочную перспективу.
Как не ошибиться и не только вернуть вложенные средства, но еще и получить прибыль от инвестиций?
Для этого можно воспользоваться одним из методов оценки эффективности инвестиционных проектов. NPV — это один из таких методов. Найти NPV инвестиционного проекта означает найти чистую приведенную стоимость всех денежных потоков, связанных с этим проектом.
Как это сделать, используя формулу для расчета NPV, и так ли это сложно, читайте ниже.
Что можно делать с деньгами?
Если у вас появилась некоторая сумма денег, то есть три возможности ими распорядиться:
- а) потратить — купить большую квартиру и жить в ней, купить автомобиль и ездить на нем на работу, съездить в отпуск на Гавайи. У каждого есть свои варианты, ведь, чтобы потратить деньги, советчики не нужны.
- б) спрятать в сейф на «черный день». И всё время трястись, что их украдут. И с грустью наблюдать, как они обесцениваются в результате инфляции
- в) «вложить» (инвестировать) куда-нибудь с целью получения дохода в будущем. А будет ли это выгодно?
Эта статья для тех, кто выбирает третий пункт из этого списка. И не важно, собираетесь ли вы инвестировать свои деньги или деньги компании, в которой вы будете работать финансовым специалистом.
Инвестировать можно в банк, положив деньги на депозит, а можно купить долговые обязательства или акции банков или компаний, которые свободно торгуются на финансовом рынке. Это самый простой путь, но не самый доходный. Для физических лиц, то есть нас с вами, чаще всего, это единственный способ вложения накоплений.
А можно инвестировать в бизнес, что означает купить долгосрочные активы (основные средства), используя которые в процессе производства, торговли или оказания услуг, вы будете получать в будущем притоки денежных средств. Для юридических лиц (компаний) это собственно говоря, и является целью их существования — делать деньги (прибыль) из инвестиций.
Чтобы определить, будет ли успешным тот или иной инвестиционный проект, финансовыми специалистами используются определенные методы оценки проектов. Два основных метода — это NPV и IRR.
NPV — что это такое? Какая логика в этом показателе?
NPV — это сокращение по первым буквам фразы «Net Present Value» и расшифровывается это как чистая приведенная (к сегодняшнему дню) стоимость. Это метод оценки инвестиционных проектов, основанный на методологии дисконтирования денежных потоков.
Если вы знаете перспективный бизнес-проект и хотите вложить в него деньги, то неплохо было бы для начала рассчитать NPV (=чистую приведенную стоимость) этого бизнес-проекта. Алгоритм расчета такой:
- 1) нужно оценить денежные потоки от проекта — первоначальное вложение (отток) денежных средств и ожидаемые поступления (притоки) денежных средств в будущем
- 2) определить стоимость капитала (cost of capital) для вас — это будет ставкой дисконтирования
- 3) продисконтировать все денежные потоки (притоки и оттоки) от проекта по ставке, которую вы оценили в п.2)
- 4) Сложить. Сумма всех дисконтированных потоков и будет равна NPV проекта
Правило: если NPV больше нуля, то проект можно принять, если NPV меньше нуля, то проект стоит отвергнуть.
Логическое обоснование метода NPV очень простое. Если NPV равно нулю, это означает, что денежные потоки от проекта достаточны, чтобы
- а) возместить инвестированный капитал и
- б) обеспечить необходимый доход на этот капитал.
Если NPV положительный, значит, проект принесет прибыль, и чем больше величина NPV, тем выгоднее/прибыльнее является данный проект. Поскольку доход кредиторов (у кого вы брали деньги в долг) фиксирован, весь доход выше этого уровня принадлежит акционерам. Если компания одобрит проект с нулевым NPV, позиция акционеров останется неизменной – компания станет больше, но цена акции не вырастет. Однако, если проект имеет положительную NPV, акционеры станут богаче.
Формула NPV — пример расчета
Формула расчета NPV выглядит сложно на взгляд человека, не относящего себя к математикам:
Где:
- n, t — количество временных периодов,
- CF — денежный поток (Cash Flow),
- R — стоимость капитала (ставка дисконтирования, Rate)
На самом деле эта формула — всего лишь правильное математическое представление суммирования нескольких величин. Чтобы рассчитать NPV, возьмем для примера два проекта А и Б, которые имеют следующую структуру денежных потоков в ближайшие 4 года:
Оба проекта А и Б имеют одинаковые первоначальные инвестиции в 10,000, но денежные потоки в последующие годы сильно разнятся. Проект А предполагает более быструю отдачу от инвестиций, но к четвертому году денежные поступления от проекта сильно упадут. Проект Б, напротив, в первые два года показывает более низкие денежные притоки, чем поступления от Проекта А, но зато в последующие два года Проект Б принесет больше денежных средств, чем проект А.
Рассчитаем NPV инвестиционного проекта следующим образом:
Предположения для упрощения расчета:
- а) все денежные потоки случаются в конце каждого года,
- б) первоначальный денежный отток (вложение денег) произошел в момент времени «ноль», т.е. сейчас
- б) стоимость капитала (ставка дисконтирования) составляет 10%
Про дисконтирование денежных потоков на этом сайте есть отдельная статья. Если расчет, приведенный ниже, вам покажется совсем непонятным, то лучше будет сначала вспомнить основы дисконтирования, вернувшись к этой статье.
Коротко напомню: чтобы привести денежный поток к сегодняшнему дню, нужно умножить денежную сумму на коэффициент 1/(1+R), при этом (1+R) надо возвести в степень, равную количеству лет. Величина этой дроби называется фактором или коэффициентом дисконтирования. Чтобы не вычислять каждый раз этот коэффициент, его можно посмотреть в специальной таблице, которая называется «таблица коэффициентов дисконтирования».
Применим формулу NPV для Проекта А. У нас четыре годовых периода и пять денежных потоков. Первый поток (10,000) — это наша инвестиция в момент времени «ноль», то есть сегодня. Если развернуть формулу NPV, приведенную чуть выше, то мы получим сумму из пяти слагаемых:
Если подставить в эту сумму данные из таблицы для Проекта А вместо CF и ставку 10% вместо R, то получим следующее выражение:
То, что стоит в делителе, можно рассчитать, но проще взять готовое значение из таблицы коэффициентов дисконтирования и умножить эти коэффициенты на сумму денежного потока.
В результате приведенная стоимость денежных потоков (NPV) для проекта А равна 788,2 доллара. Расчет NPV для проекта А можно так же представить в виде таблицы и в виде шкалы времени:
Точно таким же образом рассчитывается NPV для проекта Б.
Поскольку коэффициенты дисконтирования уменьшаются с течением времени, вклад в приведенную стоимость проекта больших (4,000 и 6,000), но отдалённых по времени (третий и четвертый годы) денежных потоков будет меньше, чем вклад от денежных поступлений в первые годы проекта. Поэтому ожидаемо, что для проекта Б чистая приведенная стоимость денежных потоков будет меньше, чем для Проекта А.
У меня получилось, что NPV Проекта Б — 491,5 доллара.
Расчет NPV для проекта Б можно посмотреть в таблице и на рисунке со шкалой времени.
Вывод: оба проекта можно принять, так как NPV обоих проектов больше нуля, а, значит, осуществление этих проектов приведет к увеличению стоимости компании-инвестора.
Если эти проекты взаимоисключающие, то есть необходимо выбрать один из них, то предпочтительнее выглядит Проект А, поскольку его NPV заметно больше 788,2, чем NPV Проекта Б 491,5.
Цифры для расчета NPV инвестиционного проекта — в чём сложность?
Применить математическую формулу несложно, если известны все переменные. Когда у вас есть все цифры — денежные потоки и стоимость капитала — то вы легко сможете подставить их в формулу и рассчитать NPV. Но не всё так просто. Реальная жизнь отличается от чистой математики тем, что невозможно точно определить величину переменных, которые входят в эту формулу. Собственно говоря, именно поэтому на практике примеров неудачных инвестиционных решений гораздо больше, чем удачных.
а) Денежные потоки
Сделать точный прогноз всех расходов и доходов, связанных с большим комплексным проектом, невероятно трудно. Например, если инвестиционный проект связан с выпуском на рынок нового товара, то для расчета NPV необходимо будет сделать прогноз будущих продаж товара в штуках, и оценить цену продажи за единицу товара. Эти прогнозы основываются на оценке общего состояния экономики, эластичности спроса (зависимости уровня спроса от цены товара), потенциального эффекта от рекламы, предпочтений потребителей, а также реакции конкурентов на выход нового продукта.
Кроме того, необходимо будет сделать прогноз операционных расходов (платежей), а для этого оценить будущие цены на сырье, зарплату работников, коммунальные услуги, изменения ставок аренды, тенденции в изменении курсов валют, если какое-то сырье можно приобрести только за границей и так далее. И все эти оценки нужно сделать на несколько лет вперед.
б) Ставка дисконтирования
Ставка дисконтирования в формуле расчета NPV — это стоимость капитала (cost of capital) для инвестора. Другими словами, это ставка процента, по которой компания-инвестор может привлечь финансовые ресурсы.
В общем случае компания может получить финансирование из трех источников:
- взять в долг (обычно у банка)
- продать свои акции
- использовать внутренние ресурсы (нераспределенную прибыль)
ЧИТАЙТЕ ТАКЖЕ: Ставка дисконтирования для инвестиционного проекта. Это WACC — средневзвешенная стоимость капитала
Финансовые ресурсы, которые могут быть получены из этих трех источников, имеют свою стоимость. И она разная! Наиболее понятна стоимость долговых обязательств (пункт 1 списка). Это либо процент по долгосрочным кредитам, который требуют банки, либо процент по долгосрочным облигациям, если компания может выпустить свои долговые инструменты на финансовом рынке. Оценить стоимость финансирования из двух остальных источников сложнее. Финансистами давно разработаны несколько моделей для такой оценки, среди них небезызвестный CAPM (Capital Asset Pricing Model). Но есть и другие подходы.
Стоимость капитала для компании (и, следовательно, ставка дисконтирования в формуле NPV) будет средневзвешенная величина процентных ставок их этих трех источников. В англоязычной финансовой литературе это обозначается как WACC — сокращение по первым буквам английской фразы Weighted Average Cost of Capital, что переводится как средневзвешенная стоимость капитала.
Зависимость NPV проекта от ставки дисконтирования
Понятно, что получить абсолютно точные величины всех денежных потоков проекта и точно определить стоимость капитала, т.е. ставку дисконтирования невозможно. В этой связи интересно проанализировать зависимость NPV от этих величин. У каждого проекта она будет разная. Наиболее часто делается анализ чувствительности показателя NPV от стоимости капитала.
Давайте рассчитаем NPV по проектам А и Б для разных ставок дисконтирования. Я сделала этот расчет в Excele, результаты приведены в таблице ниже:
Табличная форма уступает графической по информативности, поэтому гораздо интереснее посмотреть результаты на графике (нажать, чтобы увеличить изображение):
Из графика видно, что NPV проекта А превышает NPV проекта Б при ставке дисконтирования более 7% (точнее 7,2%). Это означает, что ошибка в оценке стоимости капитала для компании-инвестора может привести к ошибочному решению в плане того, какой проект из двух следует выбрать.
Кроме того, из графика также видно, что Проект Б (красная линия) является более чувствительным в отношении ставки дисконтирования. То есть NPV проекта Б уменьшается ,быстрее по мере роста этой ставки (красный график более крутой). И это легко объяснимо. В проекте Б денежные поступления в первые годы проекта невелики, со временем они увеличиваются. Но коэффициенты дисконтирования для более отдаленных периодов времени уменьшаются очень значительно. Поэтому вклад больших денежных потоков в чистую приведенную стоимость так же резко падает.
Например, можно рассчитать, чему будут равны 10,000 долларов через 1 год, 4 года и 10 лет при ставках дисконтирования 5% и 10%, то наглядно можно увидеть, как сильно зависит приведенная стоимость денежного потока от времени его возникновения:
В последнем столбце таблицы видно, что один и тот же денежный поток (10,000) при разных ставках дисконтирования отличается через год всего на 4.5%. Тогда как тот же самый по величине денежный поток, только через 10 лет от сегодняшнего дня при дисконтировании по ставке 10% будет на 37,2% меньше, чем его же приведенная стоимость при ставке дисконтирования 5%. Высокая стоимость капитала (=ставка дисконтирования) «съедает» существенную часть дохода от инвестиционного проекта в отдаленные годовые периоды, и с этим ничего не поделать. Это математика.
Именно поэтому, при оценке инвестиционных проектов денежные потоки, отстоящие от сегодняшнего дня более, чем на 10 лет, обычно не используются. Помимо существенного влияния дисконтирования, еще и точность оценки отдаленных по времени денежных потоков существенно ниже.
История с выбором между двумя проектами А и Б будет продолжена в следующих публикациях на тему методов оценки инвестиционных проектов. К сожалению, большинство статей в Интернете на эту тему написано сухо и коротко, и многие из публикаций содержат ошибки, что недопустимо.
Расчет NPV — пример в Excel
В нашем компьютерном веке стало гораздо проще делать любые расчеты. В программе Excel есть функция, с помощью которой расчет NPV можно сделать быстрее, чем по таблицам. И не нужно дисконтировать каждый поток вручную. Проще зайти в раздел Excel Формулы —> Финансовые и выбрать функцию ЧПС.
Пример расчета NPV для проекта А показан ниже:
Единственная сложность заключается в том, что эта функция дисконтирует все потоки, которые вы выберете. Если же первый поток, как в проектах А и Б рассмотренных выше, приходится на период времени ноль, то его не надо вводить в ячейку значения. Первоначальная инвестиция в сумме -10,000 нужно добавить к тому значению, которое рассчитает функцию ЧПС. В этом примере дисконтируются ячейки B3-B6 (обведено красным в таблице), по ставке 0,10 (зеленый квадратик), приведенная стоимость получается равной 10,788.2. Если вычесть из этой суммы инвестицию 10,000, то получится NPV, равная 788,2. При расчете вручную мы получили 788,4, разница 0,2 получилась в результате округлений.
Другая функция программы Excel, расположенная в том же разделе финансовых формул, ЧИСТНЗ тоже считает приведенную стоимость денежных потоков, но она может это делать для неравных промежутков времени между потоками. В ней есть дополнительная ячейка, куда можно ввести диапазон дат, соответствующих времени поступления денежных средств.
И будет вам счастье и приличный счёт в банке.
Финансовая грамотность необходима каждому человеку. Современная экономика — это сложный механизм перекачивания денег из одного кармана в другой. И нужно не только научиться зарабатывать деньги, но и вкладывать их.
Учиться быть инвесторами желательно еще до того, как у вас появятся деньги. Если в будущем вам повезет, и вы выиграете миллион долларов в лотерею, то вы должны быть готовы к этому. Если вам удастся заработать достаточные для инвестирования средства, то тем более захочется распорядиться ими так, чтобы приумножить.
Другие статьи на этом сайте из рубрики «Финансы»:
Вернуться на главную страницу
Чистая приведённая стоимость (NPV) | КАЛЬКУЛЯТОР
Чистая приведённая стоимость (ЧПС, чистая текущая стоимость, чистый дисконтированный доход, ЧДД, англ. Net present value, принятое в международной практике для анализа инвестиционных проектов сокращение — NPV) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню.
Метод чистой приведенной стоимости получил широкое применение при бюджетировании капитальных вложений и принятии инвестиционных решений. Также NPV считается лучшим критерием отбора для принятия или отклонения решения о реализации инвестиционного проекта, поскольку основывается на концепции стоимости денег во времени. Другими словами, чистая приведенная стоимость отражает ожидаемое изменение благосостояния инвестора в результате реализации проекта.
Формула NPV
Чистая приведенная стоимость проекта является суммой настоящей стоимости всех денежных потоков (как входящих, так и исходящих). Формула расчета выглядит следующим образом:


Где:
- CFt – ожидаемый чистый денежный поток (разница между входящим и исходящим денежным потоком) за период t,
- r – ставка дисконтирования,
- N – срок реализации проекта.
Ставка дисконтирования
Важно понимать, что при выборе ставки дисконтирования должна быть учтена не только концепция стоимости денег во времени, но и риск неопределенности ожидаемых денежных потоков! По этой причине в качестве ставки дисконтирования рекомендуется использовать средневзвешенную стоимость капитала (англ. Weighted Average Cost of Capital, WACC), привлеченного для реализации проекта. Другими словами, WACC является требуемой нормой доходности на капитал, инвестированный в проект. Следовательно, чем выше риск неопределенности денежных потоков, тем выше ставка дисконтирования, и наоборот.
Критерий отбора проектов
Правило принятия решения об отборе проектов при помощи NPV метода довольно прямолинейно. Нулевое пороговое значение говорит о том, что денежные потоки проекта позволяют покрыть стоимость привлеченного капитала. Таким образом, критерии отбора можно сформулировать следующим образом:
- Отдельно взятый независимый проект должен быть принят при положительном значении чистой приведенной стоимости или отклонен при отрицательном. Нулевое значение является точкой безразличия для инвестора.
- Если инвестор рассматривает несколько независимых проектов, принять следует те из них, у которых наблюдается положительный NPV.
- Если рассматривается ряд взаимоисключающих проектов, выбрать следует тот из них, у которого будет максимальная чистая приведенная стоимость.
NPV. Чистый дисконтированный доход (чистая приведенная стоимость)
Чистый дисконтированный доход (ЧДД, NPV, Net Present Value) – накопленный дисконтированный эффект за расчетный период или превышение суммарных денежных поступлений над суммарными затратами для анализируемого проекта с учетом неравноценности эффектов (а также затрат, результатов), относящихся к различным моментам времени.
Методика определения чистого дисконтированного дохода заключается в суммировании дисконтированных потоков денежных средств за расчетный период времени. Приток денежных средств дисконтируется с помощью ставки дисконта r. Формула для вычисления чистого дисконтированного дохода (NPV) имеет следующий вид:
Если инвестиционным проектом предусмотрена не разовая инвестиция, а неоднократное инвестирование в течении нескольких лет, то формула расчета NPV принимает следующий вид:
Где IC0, IC1… ICm — начальные инвестиции в течение m лет; P1, P2… Pn — доходы, которые будут поступать в течение n лет; CF — Cash Flow.
Если NPV > 0, то анализируемый инвестпроект прибыльный, его следует принять, поскольку доходы от проекта превысят затраты на его реализацию; если NPV < 0, то проект убыточный, его следует отвергнуть; если NPV = 0, то проект ни прибыльный, ни убыточный.
При сравнении нескольких вариантов осуществления инвестпроектов одинаковой продолжительности следует руководствоваться критерием максимума чистого дисконтированного дохода (NPV → max).
В Microsoft Excel есть встроенная формула расчета чистого дисконтированного дохода – ЧПС.
Проиллюстрируем применение этой функции на небольшом примере:

Расчет NPV в Excel